David Cordero
How to implement a 'Skip Intro' button in tvOS
Published on 20 Aug 2020
Even though I am one of the few persons who actually like watching series intros and never uses this button, the truth is that the ‘Skip Intro’ button introduced by Netflix a few years ago is most probably one of the most beloved features in their Apps.
Knowing that AVPlayerViewController does not allow adding interactive elements easily, and any attempt to do it might result in a lot of pain dealing with Siri Remote, I wondered how Netflix developers could have implemented this skip button in tvOS without any focus issue at all.
After some tests in playground mode, I came up with the following posibility.
The idea is simple, we can achieve this behavior by creating a ViewController with the Skip button on it, and then to present it modally as an overlay over the context of the player.
To dismiss the button, we can then dismiss the modal view controller after a few seconds (as done in the example below), or programmatically if you know when the intro actually finishes.
The main problem of adding any interactive element together with AVPlayerViewController is that because the player takes control of all the gestures triggered from Siri Remote. The gesture recognizers of any additional interactive element will conflict with the ones of the player. Using the described solution instead, the gesture recognizers of the modal view controller will take priority over the ones of the player.
You can find below the code implementing this concept. Please notice that the following code is a proof of concept and it always skips forward a fixed amount of seconds, knowing the actual duration of the series intro is out of the scope of this post.
import UIKit
import AVFoundation
import AVKit
class ThePlayerViewController: AVPlayerViewController {
override func viewDidAppear(_ animated: Bool) {
super.viewDidAppear(animated)
play(stream: URL(string: "https://devstreaming-cdn.apple.com/videos/streaming/examples/img_bipbop_adv_example_ts/master.m3u8")!)
presentSkipOverlay()
}
// MARK: - Private
private func play(stream: URL) {
let asset = AVAsset(url: stream)
let playetItem = AVPlayerItem(asset: asset)
player = AVPlayer(playerItem: playetItem)
player?.play()
}
private func presentSkipOverlay() {
let skipOverlayViewController = SkipOverlayViewController()
skipOverlayViewController.onSkip = {
[weak self] in
// Skip the intro here. For the example skip 60 seconds
self?.player?.seek(to: CMTime(seconds: 60.0, preferredTimescale: 1))
}
skipOverlayViewController.modalPresentationStyle = .overCurrentContext
skipOverlayViewController.accessibilityViewIsModal = true
present(skipOverlayViewController, animated: true, completion: {
// Dismiss the overlay automatically after a few seconds
DispatchQueue.main.asyncAfter(deadline: .now() + 5) {
skipOverlayViewController.dismiss(animated: true, completion: nil)
}
})
}
}
And this could be a naive implementation of the Overlay view controller:
final class SkipOverlayViewController: UIViewController {
var onSkip: (() -> Void)?
override func viewDidLoad() {
super.viewDidLoad()
setUpView()
}
// MARK: - Private
private lazy var skipButton: UIButton = {
let skipButton = UIButton()
skipButton.backgroundColor = .white
skipButton.setTitleColor(.black, for: .normal)
skipButton.setTitle("Skip Intro", for: .normal)
skipButton.addTarget(self, action: #selector(skipButtonWasPressed), for: .primaryActionTriggered)
return skipButton
}()
private func setUpView() {
view.addSubview(skipButton)
skipButton.translatesAutoresizingMaskIntoConstraints = false
skipButton.trailingAnchor.constraint(equalTo: view.safeAreaLayoutGuide.trailingAnchor).isActive = true
skipButton.bottomAnchor.constraint(equalTo: view.safeAreaLayoutGuide.bottomAnchor, constant: -200).isActive = true
skipButton.widthAnchor.constraint(equalToConstant: 225).isActive = true
}
// MARK: - Actions
@objc
func skipButtonWasPressed() {
onSkip?()
}
}
Here you have the result:
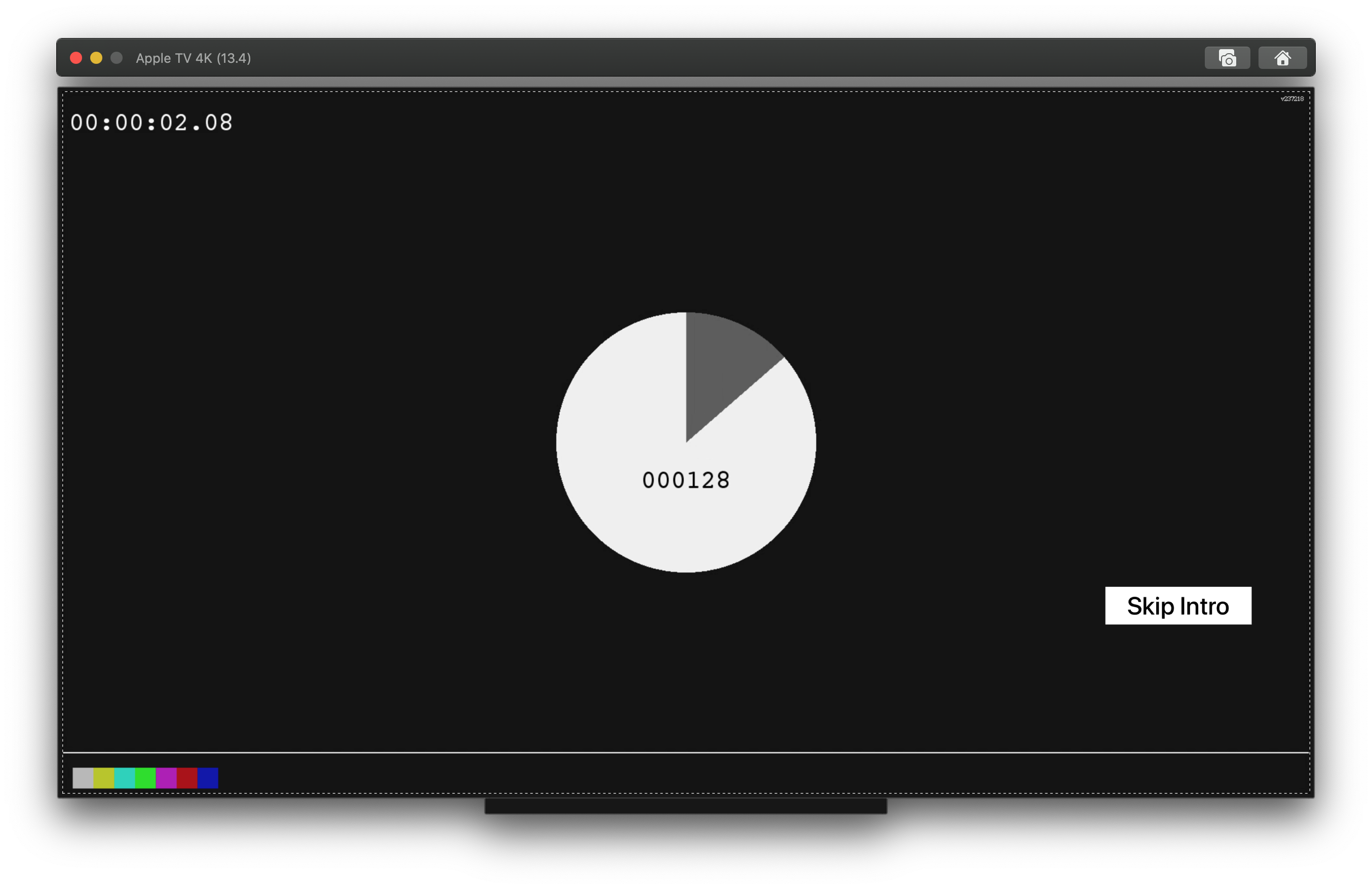
Depending on your use cases, it might be useful to create an extension helper for AVPlayerViewController to ease the presentation of the overlay from any player.
extension AVPlayerViewController {
func presentSkipOverlay() {
let skipOverlayViewController = SkipOverlayViewController()
skipOverlayViewController.onSkip = {
[weak self] in
// Skip the intro here. For the example skip 60 seconds
self?.player?.seek(to: CMTime(seconds: 60.0, preferredTimescale: 1))
}
skipOverlayViewController.modalPresentationStyle = .overCurrentContext
skipOverlayViewController.accessibilityViewIsModal = true
present(skipOverlayViewController, animated: true, completion: {
DispatchQueue.main.asyncAfter(deadline: .now() + 5) {
skipOverlayViewController.dismiss(animated: true, completion: nil)
}
})
}
}
Disclaimer
The code in this post is a proof of concept, do not copy and paste this code to your App without understanding what the code does. You should actually never do that…
If you need to implement a ‘Skip button’ in your App, analyze this code, get the idea behind the implementation, and then implement it by yourself.
⚠️ Note
At WWDC2021 Apple has introduced a new option to add contextual action buttons in AVPlayerViewController from tvOS 15. You can find more info about this in the following presentation: